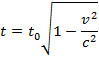Paul Davies, divulgador científico

Paul Davies

The same post in English

Paul Davies pasó al primer plano entre los científicos que dedican tiempo a la divulgación con su libro, publicado en 1992, La Mente de Dios (The Mind of God), escrito en respuesta a las últimas palabras de Stephen Hawking en su best-seller divulgativo Breve Historia del Tiempo (A Brief History of Time). En otro artículo hablé de otro de sus libros de divulgación, Un Silencio Inquietante (The Eerie Silence). Aquí voy a hablar de otros dos libros suyos.

Los últimos tres minutos (The Last Three Minutes, 1994): Este libro de divulgación está un poco atrasado, pues es anterior al modelo cosmológico estándar, pero explica bien cómo estaba la cosmología cuando se publicó el libro, y muchas de las cosas que dice siguen siendo válidas. Dice algo interesante: que la teoría del Big Bang de Lemaître (a quien Davies no nombra) debería haber sido aceptada mucho antes de que sus dos predicciones acertadas sorprendentes le dieran el espaldarazo en los años 60, porque hay otro argumento que la apoya, y que los científicos del siglo XIX debieron haber notado, pero no lo hicieron: Si el universo fuera infinitamente antiguo, ya habría muerto. Es evidente que, si algo tiende a detenerse con una tasa finita, no puede haber existido desde toda la eternidad. Por cierto, en el párrafo citado comete un error: ignora la diferencia entre eternidad y perpetuidad, que resolvió Boecio hace un milenio y medio. Hay también un fallo importante cuando dice que el radio del cosmos visible es de 15.000 millones de años-luz, porque no tiene en cuenta la expansión del universo. El radio correcto es de unos 43.000 millones de años-luz. A esto hay que sumar algún error cometido por el traductor al español, como traducir silicon como silicona (la traducción correcta es silicio). En cambio, ha traducido correctamente los números muy grandes (billón, trillón, cuatrillón...), uno de los errores típicos de los traductores del inglés americano al español.

Mis diez descubrimientos científicos favoritos del siglo XX

The same post in English

En un artículo publicado hace dos semanas comenté la contestación dada en un artículo de la revista Science News a la pregunta de cuáles han sido los diez descubrimientos científicos más importantes del último siglo. Alguno de mis lectores me ha preguntado cuál es mi opinión personal al respecto. Contesto aquí.

Para empezar, señalaré que la investigación científica puede avanzar por cuatro caminos diferentes:

1. La ciencia teórica, que trata de descubrir leyes fundamentales en el universo.
2. La ciencia experimental, que confirma o falsa las teorías, realizando experimentos.
3. La ciencia observacional, que en lugar de experimentar observa. La astronomía, por ejemplo, utiliza estos métodos, pues la experimentación casi nunca es posible.
4. La tecnología, la aplicación práctica de la ciencia, cuyo objetivo es construir dispositivos que funcionen.

Los límites de las matemáticas

Kurt Gödel

The same post in English

A finales del siglo XIX, Friedrich Ludwig Gottlob Frege, profesor de la universidad de Viena, emprendió un programa ambicioso: formalizar la aritmética mediante unos pocos axiomas y unas pocas reglas de deducción, de modo que todo teorema verdadero pudiese deducirse de los axiomas mediante cierto número de aplicaciones de las reglas de deducción. El resultado fue un libro monumental, Grundgesetze der Arithmetike (1893-1903), que entre otras cosas formalizó la teoría de conjuntos con una notación engorrosa, que pronto fue sustituida por la de Peano, que es la que usamos ahora.

Desgraciadamente para Frege, cuando estaba a punto de publicarse el segundo tomo de su libro, Bertrand Russell le envió una carta en la que demostraba que su formulación de la teoría de conjuntos daba pie a una inconsistencia. En la teoría de Frege, un conjunto puede pertenecer a otro conjunto. En particular, algunos conjuntos no pertenecen a sí mismos (como el conjunto de los números enteros, que no es un número entero), mientras otros sí pertenecen a sí mismos (como el conjunto de todos los conjuntos infinitos, que es infinito). Russell señaló que es posible definir el conjunto de todos los conjuntos que no pertenecen a sí mismos. Este conjunto lleva a una paradoja: si pertenece a sí mismo, no pertenece, y viceversa. La paradoja de Russell acabó con la obra de Frege, que tuvo que añadir apresuradamente un apéndice a su libro y abandonó la investigación sobre los fundamentos de las matemáticas.

Teología matemática

The same post in English

Ernst Zermelo

Ernst Zermelo (1871-1953) fue un matemático famoso de principios del siglo XX. Entre sus logros, podemos mencionar los siguientes:

• En 1899 descubrió la paradoja de Russell, dos años antes que Russell. Aunque no la publicó, sí la comentó con sus colegas de la Universidad de Göttingen, entre los que estaba David Hilbert. La paradoja de Russell demuestra que la teoría de conjuntos de Cantor es inconsistente, pues permite construir el conjunto de todos los conjuntos que no pertenecen a sí mismos. Veamos: hay conjuntos que no pertenecen a sí mismos, como el de los números pares; ese conjunto no es un número par. Otros sí pertenecen a sí mismos, como el conjunto de los conjuntos infinitos, que es un conjunto infinito. Ahora nos preguntamos: ¿Pertenece a sí mismo el conjunto de todos los conjuntos que no pertenecen a sí mismos? Esta pregunta nos lleva a una paradoja: si pertenece, no pertenece; y si no pertenece, sí pertenece.
• En 1904 demostró el teorema del buen orden, como primer paso hacia la demostración de la hipótesis del continuo, el primero de los 23 problemas sin resolver de Hilbert. El teorema del buen orden afirma que todo conjunto puede ser bien ordenado, lo que quiere decir que todo subconjunto ordenado no vacío debe tener un elemento mínimo. Para demostrarlo, propuso el axioma de elección, del que hablaremos a continuación.
• En 1905 comenzó a trabajar en la axiomatización de la teoría de conjuntos. Su sistema, mejorado en 1922 por Adolf Fraenkel, es un conjunto de 8 axiomas, que hoy se llama sistema de Zermelo-Fraenkel (ZF). Añadiendo a este sistema el axioma de elección, obtenemos el sistema ZFC, el más utilizado hoy día en la teoría de conjuntos.

Gödel y el realismo

The same post in English

Kurt Gödel

Kurt Gödel (1906-1978) fue uno de los matemáticos más importantes del siglo XX. En 1931, cuando tenía 25 años, saltó a la fama al demostrar matemáticamente que el intento de construir un sistema axiomático completo a partir del cual pueda deducirse toda la aritmética de los números naturales, o cualquier sistema equivalente, está condenado al fracaso.

Su primer teorema de incompletitud dice esto:

Todo sistema formal consistente y con potencia semejante a la de la aritmética elemental, no es completo (contiene proposiciones verdaderas indecidibles).

Veamos una demostración informal simplificada:

Sea el Teorema G, que dice lo siguiente: Este teorema G no se puede demostrar partiendo de los axiomas y las reglas del sistema S.

• Si suponemos que el teorema G es falso, el sistema S es inconsistente, pues a partir de los axiomas y reglas de S se podría demostrar un teorema falso.
• Luego si S es consistente, G tiene que ser verdadero, y por tanto no se puede demostrar a partir de los axiomas de S.
  

El teorema de Gödel demuestra que toda formalización axiomática de la aritmética, o bien es inconsistente (permite demostrar teoremas falsos), o bien es incompleta (contiene teoremas verdaderos que no se pueden demostrar).

¿Qué dice la física sobre los viajes en el tiempo?

The same post in English

En el artículo anterior planteamos algunas paradojas que nos podrían hacer dudar sobre la posibilidad de realizar viajes en el tiempo. Pero ¿qué dice la física? ¿Hay alguna teoría que haga posible viajar en el tiempo? ¿Es verdad, como dicen algunos, que la teoría especial de la relatividad de Einstein implica que será posible viajar en el tiempo?

En primer lugar, es preciso refutar una idea falsa, pero bastante extendida. A menudo se oye decir algo parecido a esto:

Si fuese posible viajar a velocidades mayores que la de la luz, viajaríamos hacia atrás en el tiempo, porque el tiempo transcurrido sería negativo.

¿Es esto cierto? Veamos la ecuación que define la relación entre el tiempo propio y el tiempo externo para un cuerpo que se mueve con movimiento rectilíneo y uniforme, de acuerdo con la teoría especial de la relatividad:

Donde t es el tiempo vivido por los viajeros que se mueven a la velocidad v; t₀ es el tiempo externo equivalente (el tiempo experimentado por un objeto que se encuentre en reposo); y c es la velocidad de la luz. Podemos ver que, para v < c, el término que está dentro de la raíz cuadrada es positivo y menor que 1, su raíz también lo será, y por lo tanto t < t₀ (el tiempo de los viajeros se acorta).